Biến đổi Khí hậu Có Thể Thay Đổi Độ Dài Ngày năm 2025?

Ngày 29 tháng 6 năm 2022, là ngày ngắn nhất từ trước đến nay, ít hơn 1,59 mili giây so với 24 giờ. Có lẽ bạn không chú ý, vì 1,59 mili giây trôi qua khá nhanh, nhưng nó đặt ra một số câu hỏi lý thuyết thú vị, như: Vì nó rơi vào một ngày thứ Tư, liệu bạn có nên trừ đi 1,59 mili giây đó từ ngày làm việc hay từ giấc ngủ của bạn? Và: Liệu ngày trên Trái đất có thể trở nên ngắn hơn không?

Đó có vẻ như một ý tưởng hoang đường, nhưng có một lý do để nghĩ rằng điều đó có thể xảy ra: biến đổi khí hậu. Việc đốt cháy nhiên liệu hóa thạch thêm carbon dioxide vào khí quyển, làm tan chảy các dãy núi lớn - và cách mà điều này ảnh hưởng đến chuyển động của Trái đất có thể ảnh hưởng đến độ dài của một ngày. Tôi sẽ hướng dẫn bạn từng bước.

Ngày Là Gì?

Đầu tiên, hãy tìm hiểu một số cơ bản về cách chúng ta xác định một “ngày” là gì. Chúng ta sẽ bắt đầu với mặt trời. Vì mục đích tính toán này, chúng ta có thể giả định rằng mặt trời chỉ đứng ở một chỗ. Tất nhiên, điều này không phải là sự thật - thực tế, mặt trời quay quanh trung tâm của dải ngân hà. Nhưng chuyển động này không có ảnh hưởng đo được đến độ dài của một ngày.

Trái đất có hai chuyển động làm thay đổi độ dài của một ngày. Đầu tiên, hành tinh quay quanh mặt trời, một quỹ đạo mất một năm. Thứ hai, nó quay quanh một trục từ cực bắc đến cực nam. Mỗi vòng quay mất khoảng một ngày. Trục quay của Trái đất không chính xác nằm vuông góc với mặt phẳng quỹ đạo. Thay vào đó, nó nghiêng khoảng 23,4 độ.

Có nhiều định nghĩa về “ngày”—có lẽ nhiều hơn bạn nghĩ. Tất nhiên, có cảm nhận thông thường về ngày so với đêm, trong đó ngày có nghĩa là phần của chu kỳ mặt trời khi vị trí của bạn trên Trái đất đối diện với mặt trời và nó sáng. Sử dụng định nghĩa đó, khá rõ ràng rằng độ dài của một ngày không đều—chắc chắn bạn đã chú ý rằng ánh sáng ban ngày ngắn hơn vào mùa đông và dài hơn vào mùa hè. Sự khác biệt này là do nghiêng của trục quay của Trái đất. Trong mùa hè, bán cầu bắc nghiêng về phía mặt trời. Điều này có nghĩa là mặt trời mọc cao hơn trên bầu trời và đi một đường dài từ bình minh đến hoàng hôn, vì vậy có thêm thời gian ánh sáng ban ngày. Đối với bán cầu bắc, ngược lại xảy ra vào mùa đông. (Các mùa đối lập ở bán cầu nam.)

Nhưng đây không phải là loại ngày chúng ta muốn nói về. Có hai định nghĩa khác chúng ta có thể sử dụng. Một là thời gian từ buổi trưa một ngày đến buổi trưa hôm sau—định nghĩa “buổi trưa” là khi mặt trời đạt đến điểm cao nhất trên bầu trời. Đây được gọi là ngày mặt trời, và nó có giá trị là 24 giờ, hoặc 86.400 giây.

Điều này có nghĩa là Trái đất mất 24 giờ để thực hiện một vòng quay đầy đủ chứ? Thực tế, không phải vậy. Trái đất thực hiện một vòng quay trong 23 giờ, 56 phút và khoảng 4 giây. Khoảng thời gian ngắn này được gọi là ngày sao. Bạn có thể định nghĩa nó là thời gian mà một ngôi sao bạn quan sát trên bầu trời mất để quay lại cùng một vị trí rõ ràng từ góc nhìn của bạn trên Trái đất. Tại sao điều này khác biệt so với ngày mặt trời? Đó là vì Trái đất đang xoay quanh trục của mình và quay quanh mặt trời cùng một lúc.

Hãy xem xét một ví dụ với một hành tinh ảo. Trong hệ mặt trời này, hành tinh hoàn thành một quỹ đạo quanh mặt trời trong 8,6 ngày mặt trời, thay vì 365 ngày như Trái đất. (Tôi đang sử dụng một năm ngắn hơn vì nó làm to lên sự khác biệt giữa ngày mặt trời và ngày sao, để bạn có thể nhìn thấy nó dễ dàng hơn.)

Dưới đây là một đoạn hoạt hình cho thấy sự khác biệt giữa ngày mặt trời và ngày sao cho hành tinh này. Mũi tên chỉ ra khi một điểm nhất định trên hành tinh trỏ vào một ngôi sao xa xôi (nằm ngoài khung hình) hoặc vào mặt trời của nó. Thời điểm chính xác khi nó trỏ vào mặt trời là khi mặt trời sẽ ở điểm cao nhất trên bầu trời đối với một người quan sát ở điểm đó.

Chú ý rằng đối với một ngày sao, hành tinh thực sự thực hiện một vòng quay đầy đủ—với một khoảng thời gian là 0,648 “đơn vị thời gian.” (Trong ví dụ này, tôi cũng tạo ra các đơn vị thời gian ảo.) Tuy nhiên, tại điểm này trong chuyển động, mặt trời không quay lại chỗ cũ trong bầu trời của hành tinh, vì trong ngày sao đó hành tinh đã di chuyển. Mất 0,726 “đơn vị thời gian” trước khi mũi tên trỏ lại mặt trời. Vì vậy, trong trường hợp này, ngày mặt trời ngắn hơn một chút so với ngày sao, giống như trên Trái đất.

Có thể ngày mặt trời ngắn hơn so với ngày sao không? Dạ có. Nếu hành tinh xoay theo hướng ngược lại với quỹ đạo quay của nó, thì quay ngược này sẽ đưa mặt trời trở lại điểm cao nhất sớm hơn. Dưới đây là cái nhìn về điều đó:

Tuy nhiên, do cách hệ mặt trời hình thành, hành tinh thường xoay theo cùng hướng với quỹ đạo quay của chúng. Trong hệ mặt trời của chúng ta, chỉ có Sao Kim xoay ngược. (Ồ, Sao Thiên Vương xoay nằm nghiêng—tôi không chắc liệu có tính là xoay ngược không.) Nhưng điều quan trọng là ngày mặt trời khác biệt so với ngày sao.

Biến đổi trong một Ngày Mặt Trời

Đối với hành tinh tưởng tượng của chúng ta, độ dài của mỗi ngày mặt trời giống nhau như ngày mặt trời trước đó. Trên Trái đất, điều này không đúng. Sự khác biệt là hành tinh tưởng tượng của chúng ta có quỹ đạo tròn, trong khi quỹ đạo của Trái đất không hoàn toàn tròn—gần tròn, nhưng không chính xác.

Dưới đây là cái nhìn về hành tinh tưởng tượng với quỹ đạo elip. Lưu ý: Tôi không hiển thị sự quay của hành tinh quanh trục của nó. Thay vào đó, tôi có một mũi tên vectơ màu đỏ để đại diện cho vận tốc của hành tinh—càng dài mũi tên, hành tinh di chuyển càng nhanh.

Chú ý rằng khi hành tinh gần Mặt Trời hơn, nó tăng tốc. Sau đó, nó chậm lại khi xa Mặt Trời hơn. Có một vài cách để giải thích hiện tượng này, nhưng tôi sẽ sử dụng ý tưởng về động lượng góc.

Nói trung thực, toán học cần thiết để hiểu đầy đủ về động lượng góc có thể trở nên phức tạp. Vì vậy, thay vào đó, tôi chỉ sẽ giải thích điều này bằng một bài thực hành thú vị.

Hãy tưởng tượng bạn đang ngồi trên một chiếc ghế văn phòng có thể xoay quanh. Bạn tự quay bằng cách đẩy chân vào sàn. Sau đó, bạn nâng chân lên khỏi mặt đất và quay như cuộc sống của bạn phụ thuộc vào nó. Bạn cảm thấy như bạn là vị vua của thế giới trong chiếc ghế xoay của mình, vì vậy bạn vươn ra hai tay như Leo Dicaprio trên đỉnh con tàu Titanic. Sau đó, bạn bắt đầu cảm thấy chói lọi, vì vậy bạn rút tay lại. Đoán xem điều gì sẽ xảy ra?

Khi bạn rút tay vào, bạn tăng tốc độ quay của mình. Nhưng động lượng góc của bạn không thay đổi. Trong ví dụ này, động lượng góc (L) là tích của vận tốc quay (ω) và một thứ gọi là khả năng quán tính (I).

OK, một vài ý kiến. Đầu tiên, các nhà vật lý sử dụng chữ cái không rõ nghĩa L cho động lượng góc vì chỉ có nhiều chữ cái để lựa chọn và “a” đã được sử dụng cho gia tốc. Điều này có nghĩa là chúng ta có thể viết động lượng góc như sau:

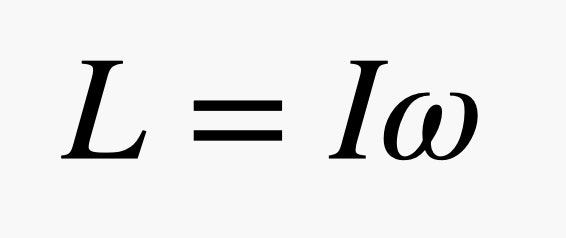
Ngoài ra, thuật ngữ “khả năng quán tính” không mô tả được và có thể là phần khó nhất để hiểu. Đây là một lượng phụ thuộc không chỉ vào khối lượng của một đối tượng mà còn vào cách phân phối khối lượng đó xung quanh trục quay.

Nếu bạn giữ tay vươn ra xa cơ thể, bạn có hai khối lượng ở xa khỏi trục quay (chạy qua trung tâm cơ thể). Khi bạn rút tay vào gần, khoảng cách từ trung tâm đến những khối lượng này giảm đi, điều này làm giảm khả năng quán tính của bạn. Với sự giảm khả năng quán tính, cách duy nhất để động lượng góc của bạn duy trì không đổi là tăng vận tốc quay của bạn. Có thể xảy ra thay đổi trong động lượng góc—như khi bạn đẩy chân vào sàn để bắt đầu quay ghế. Nhưng một khi chân bạn không còn chạm đất, động lượng góc của bạn là không đổi.

Liên quan đến một ngày mặt trời của một hành tinh quay quanh một ngôi sao là gì? Khi hành tinh di chuyển gần ngôi sao, moment quán tính của nó giảm, giống như khi bạn kéo cánh tay về phía cơ thể khi ngồi trên chiếc ghế quay. Mô-men góc của hệ thống này có giá trị không đổi, vì vậy sự giảm moment quán tính này có nghĩa là hành tinh phải di chuyển nhanh hơn.

Dưới đây là một mô hình của hành tinh quay ảo đó có quỹ đạo không hình tròn. Mỗi khi mặt trời quay lại vị trí giống nhau trên bầu trời, tôi sẽ vẽ một đường đến mặt trời, để bạn có thể thấy khi nào diễn ra ngày mặt trời.

Khi hành tinh di chuyển gần mặt trời, nó di chuyển với tốc độ cao hơn. Điều này có nghĩa là khi quay quanh trục của nó, nó đi qua một góc lớn hơn, đồng nghĩa với việc nó phải quay thêm một lượng nhiều hơn để đưa mặt trời về cùng một vị trí. Do đó, ngày mặt trời sẽ kéo dài hơn khi hành tinh ở gần mặt trời.

Chỉ để vui, đây là biểu đồ về độ dài của ngày mặt trời trong ba năm hoặc ba quỹ đạo:

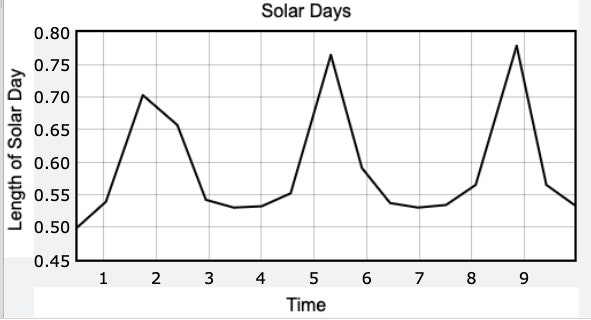
Đối với quỹ đạo của Trái Đất, sự chênh lệch về độ dài của một ngày không quá đáng chú ý. Sự biến đổi trong ngày mặt trời là khoảng 7.9 giây dài hơn hoặc ngắn hơn, tùy thuộc vào vị trí của Trái Đất trong quỹ đạo của nó.

Ngày Sao Lớn Cũng Có Thể Thay Đổi

OK, vì sự thay đổi trong chuyển động quỹ đạo của hành tinh, ngày mặt trời không còn là hằng số. Nhưng tốc độ quay thực tế của Trái Đất cũng có thể thay đổi—điều này có nghĩa là ngày sao lớn cũng không còn là hằng số nữa.

Thực sự có ba cách để thay đổi tốc độ quay của Trái Đất (và do đó làm thay đổi độ dài của một ngày sao lớn), và tất cả đều liên quan đến moment góc. Cách đầu tiên là áp dụng một mô-men xoắn lên nó. Hãy nhớ lại ví dụ về chiếc ghế văn phòng quay. Khi bạn đặt chân lên sàn và đẩy, chân bạn xoay chiếc ghế, tạo ra một mô-men xoắn. Độ lớn của một mô-men xoắn phụ thuộc cả vào cách bạn đẩy mạnh và cách lực từ xa so với điểm quay. (Chúng ta gọi đó là khoảng cách “tay xoắn.”) Một tay xoắn dài có nghĩa là bạn sẽ có một mô-men xoắn lớn hơn. Đó là lý do tay nắm cửa nằm xa khỏi bản lề cửa càng xa càng tốt—để bạn có thể áp dụng một mô-men xoắn lớn với một lực nhỏ.

Một mô-men xoắn thay đổi moment góc của một vật. Chân bạn đặt lên sàn khiến chiếc ghế từ không có moment góc (hoặc không quay) chuyển sang một giá trị khác không. Bạn cũng có thể sử dụng chân bạn để ngăn chiếc ghế quay. Trong cả hai trường hợp này, mô-men xoắn gây ra sự thay đổi moment góc. Nếu Trái Đất có một sự thay đổi moment góc, điều đó có thể đồng nghĩa với sự thay đổi vận tốc góc, từ đó làm thay đổi độ dài của một ngày sao lớn.

Có bao giờ Trái Đất trải qua mô-men xoắn không? Có. Mô-men xoắn đáng chú ý nhất trên Trái Đất đến từ mặt trăng. Có một tương tác lực hấp dẫn giữa các phần của mặt trăng và các phần của Trái Đất, vì cả hai cơ thể đều có khối lượng. Nếu cả hai đều có phân phối khối lượng đồng đều, lực rút từ tương tác lực hấp dẫn sẽ tạo ra một mô-men xoắn tổng cộng bằng không.

Tuy nhiên, cả hai đều không đều đặn. Chúng có các phần có khối lượng nhiều hơn và các phần có khối lượng ít hơn. Điều này có nghĩa là khi mặt trăng di chuyển quanh Trái Đất, nó tạo ra một mô-men xoắn khác không và giảm moment góc của nó. Theo thời gian, moment góc của Trái Đất sẽ tiếp tục giảm cho đến khi chỉ một mặt của hành tinh hướng về mặt trăng—giống như chỉ một mặt của mặt trăng hướng về Trái Đất. Điều này, vào một lúc nào đó, làm cho độ dài của một ngày sao lớn khoảng 28 ngày. (Đừng lo, điều này sẽ không xảy ra trong thời gian sớm.)

Một cách khác để thay đổi chiều dài của một ngày trên ngôi sao là thông qua sự chuyển giao của moment góc. Hãy tưởng tượng bạn là một phi hành gia đang thực hiện công việc ngoài vũ trụ, và vì một lý do nào đó bạn đang nắm một chiếc bánh xe đạp đang quay. Bây giờ bạn sử dụng tay để làm chậm lại quay của chiếc bánh xe. Với sự giảm tốc độ góc của bánh xe, moment góc của hệ thống bao gồm phi hành gia (bạn) và bánh xe cũng sẽ giảm.

Nhưng chờ đã! Bạn đang ở trong không gian và không có mô-men xoắn nào đi kèm với sự giảm moment góc đó. Vậy nên, bạn biết điều gì xảy ra không? Bạn bắt đầu quay khi bánh xe chậm lại. Với sự tăng tốc quay của người, tổng moment góc giữ nguyên. Đây chính là điều chúng ta muốn nói khi nói về "chuyển giao của moment góc" — nói một cách nào đó, moment góc từ bánh xe đạp được chuyển sang moment góc của bạn, người phi hành gia đang quay.

Trái đất hơi giống như một phi hành gia có một chiếc bánh xe đang quay. Nó có hai phần có thể quay với tốc độ khác nhau — vỏ trái đất (phần cứng mà bạn sống trên đó) và lõi ngoại (làm từ kim loại sắt-niken lỏng). Với địa chất này, có thể xảy ra sự quay khác nhau giữa lõi và vỏ. Mọi thay đổi trong sự quay của lõi lỏng sẽ tạo ra một thay đổi tương ứng trong sự quay của vỏ. Vì chúng ta đo một ngày trên ngôi sao dựa trên sự quay của vỏ, chuyển giao này của moment góc sẽ thay đổi chiều dài của một ngày.

Cách cuối cùng để thay đổi chiều dài của một ngày trên ngôi sao là thay đổi độ nhất quán với moment của Trái Đất đang quay. Điều này giống như khi một vận động viên trượt băng đang quay nhanh kéo cánh tay vào phía cơ thể. Khi cánh tay được coi lại, độ nhất quán của họ sẽ giảm. Tuy nhiên, với không có mô-men xoắn trên hệ thống, giảm độ nhất quán sẽ đồng nghĩa với việc tăng tốc độ góc.

Tất nhiên, Trái Đất không có cánh để kéo gần bề mặt của nó. Tuy nhiên, nó có các tảng băng, thường nằm trong các dãy núi. Khi một tảng băng núi tan chảy, nước kết quả không chỉ đứng yên trên núi. Nó chảy xuống dốc gần bề mặt của Trái Đất — có phần giống như một vận động viên trượt băng co cơ thể về phía trong. Và như bạn biết, việc tảng băng tan chảy có thể là một hậu quả của biến đổi khí hậu.

Hãy xem xét tác động mà điều đó có thể gây ra đối với chiều dài của một ngày.

Ước Lượng Sự Thay Đổi Do Tảng Băng

Bởi vì có nhiều yếu tố đóng góp vào tốc độ góc của Trái Đất, việc tính toán đầy đủ tất cả các yếu tố góp phần vào việc tạo ra "ngày ngắn nhất từ trước đến nay" là khó khăn.

Vì vậy, tôi sẽ xem xét tác động của một điều duy nhất — sự tan chảy của tảng băng. Hãy bắt đầu với Trái Đất quay một lần mỗi 86,400 giây, tức là một ngày mặt trời, và giả sử có các tảng băng với đá băng đóng ở đỉnh một số ngọn núi. Tôi cần ước lượng moment quán tính của Trái Đất (I_E) với các tảng băng có khối lượng m_g ở đỉnh các núi — cách trục quay một khoảng r_g1. Sau đó, tôi cần tìm moment quán tính khi nước từ tảng băng tan chảy lại ở một khoảng cách ngắn hơn là r_g2 — khoảng cách của nước này từ trục quay khi nó ở mực nước biển.

Lưu ý rằng giá trị này của r là khoảng cách từ tảng băng đến trục quay (một đường ảo chạy từ cực bắc đến cực nam). Nếu một tảng băng ở xích đạo, giá trị r này sẽ là bán kính của Trái Đất cộng với chiều cao của ngọn núi. Tuy nhiên, nếu bạn di chuyển đến vĩ độ cao hơn, giá trị r sẽ nhỏ hơn bán kính của Trái Đất. Có lẽ sơ đồ này sẽ giúp:

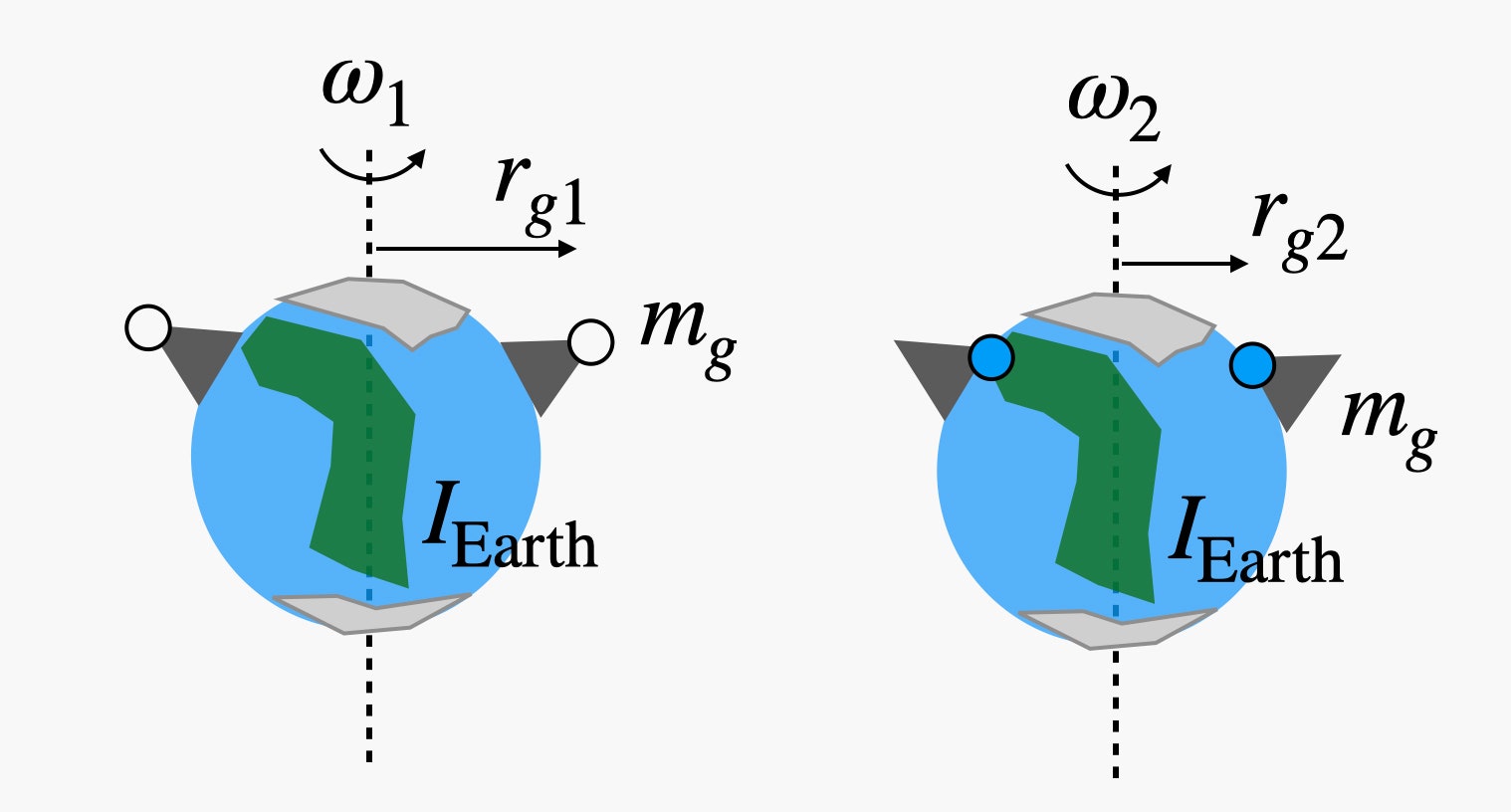
Nếu tôi biết khối lượng của các tảng băng, cùng với khoảng cách ban đầu và cuối cùng, thì phương trình bảo toàn moment góc sẽ trông như thế này:

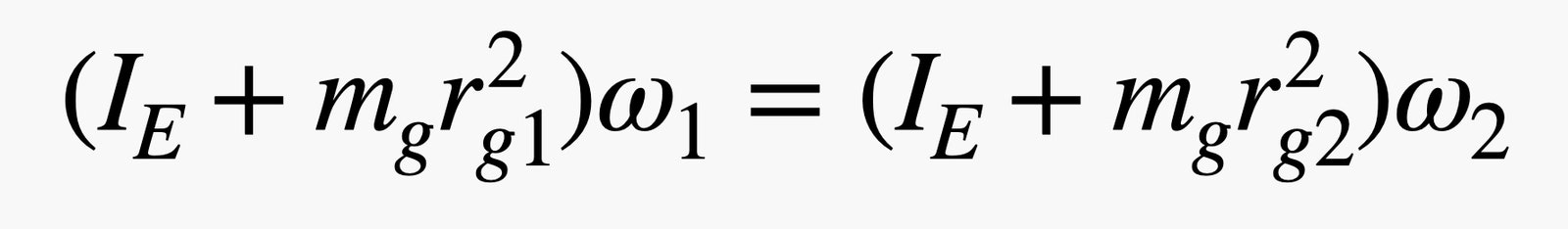
Vâng, nó trông khó khăn, nhưng đừng lo. Quan trọng là nếu tôi ước lượng một số thông số, tôi có thể tính toán được giá trị của vận tốc góc cuối cùng.

Trước hết, mặc dù có một phương trình cho moment quán tính của một quả cầu đồng nhất, Trái Đất không đồng nhất và không hoàn toàn rắn. Trong bài tập này, tôi sẽ ước lượng moment quán tính cho Trái Đất là ⅖MR² (trong đó M và R là khối lượng và bán kính của Trái Đất) và sau đó thêm một yếu tố điều chỉnh, điều này nên là đủ tốt.

Khối lượng của tảng băng tan chảy phức tạp hơn một chút. Theo một nghiên cứu, có khoảng 215,000 tảng băng trên Trái Đất với tổng thể tích khoảng 159 x 10³ kilômét khối. Tất nhiên, nếu chúng ta biết thể tích, thì chúng ta có thể có được khối lượng bằng cách sử dụng mật độ đá băng là 917 kilôgam trên mét khối.

Còn một điều cần xem xét: Tảng băng tan chảy ở cực bắc và cực nam (và ở khu vực Bắc Cực) thực sự sẽ không ảnh hưởng đến moment quán tính. Vì chúng đã rất gần trục quay, nước tan chảy và di chuyển gần tâm của Trái Đất sẽ không thay đổi giá trị r của chúng. Thực tế, chỉ khoảng 10,3 phần trăm thể tích tảng băng ước lượng này sẽ đóng góp một cách đáng kể vào sự thay đổi moment quán tính.

Nhưng chỉ để vui thôi, hãy nói rằng tất cả băng này đều ở vĩ độ 45 độ (đó là ở giữa giữa xích đạo và cực), ở độ cao 5,000 mét so với mực nước biển. Với tất cả đó, tôi có các tính toán sau đây. (Bạn có thể xem tất cả chi tiết trong đoạn mã Python này.)

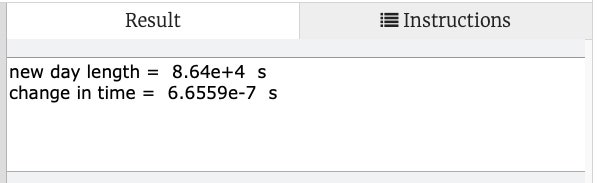
Đây là kết quả: Nếu tảng băng này tan chảy, ngày sẽ ngắn đi 0.67 micro giây, hoặc 6.67 x 10^-7 giây. Đó không phải là một sự khác biệt lớn, nhưng đó là một sự khác biệt. Và trong khi mất đi một phần nhỏ của một giây trong chiều dài của một ngày không đáng kể so với tàn phá môi trường do tảng băng tan chảy, tôi hy vọng điều này sẽ không xảy ra.