Cuối cùng, một vấn đề chỉ có thể được giải quyết bởi máy tính lượng tử năm 2026

Ngay từ những ngày đầu tiên của nghiên cứu về máy tính lượng tử, các nhà khoa học máy tính đặt ra một câu hỏi, câu trả lời của nó sẽ tiết lộ điều gì đó sâu sắc về sức mạnh của những máy tính tương lai này. Hai mươi lăm năm sau đó, vấn đề đã được giải quyết gần như hoàn toàn. Trong một bài báo đăng trực tuyến vào cuối tháng 5, các nhà khoa học máy tính Ran Raz và Avishay Tal cung cấp bằng chứng mạnh mẽ cho việc máy tính lượng tử có khả năng tính toán vượt xa mọi thứ mà máy tính cổ điển có thể đạt được.
Raz, một giáo sư tại Đại học Princeton và Viện Khoa học Weizmann, và Tal, một nghiên cứu viên sau tiến sĩ tại Đại học Stanford, định nghĩa một loại vấn đề tính toán cụ thể. Họ chứng minh, với một số điều kiện nhất định, rằng máy tính lượng tử có thể xử lý vấn đề một cách hiệu quả trong khi máy tính truyền thống sẽ bế tắc mãi mãi khi cố gắng giải quyết nó. Các nhà khoa học máy tính đã tìm kiếm một vấn đề như vậy từ năm 1993, khi họ đầu tiên định nghĩa một loại vấn đề được biết đến là “BQP,” bao gồm tất cả các vấn đề mà máy tính lượng tử có thể giải quyết.
Kể từ đó, các nhà khoa học máy tính hy vọng so sánh BQP với một loại vấn đề được biết đến là “PH,” bao gồm tất cả các vấn đề có thể được giải quyết bởi bất kỳ máy tính cổ điển nào—kể cả những máy tính cực kỳ tiên tiến được xây dựng bởi một dân tộc văn minh tương lai không thể lường trước. Việc so sánh đó phụ thuộc vào việc tìm ra một vấn đề có thể được chứng minh thuộc BQP nhưng không thuộc PH. Và bây giờ, Raz và Tal đã làm được điều đó.
Kết quả không làm tăng tầm quan trọng của máy tính lượng tử so với máy tính cổ điển theo bất kỳ ý nghĩa thực tế nào. Một điều là, các nhà khoa học máy tính lý thuyết đã biết từ trước rằng máy tính lượng tử có thể giải quyết bất kỳ vấn đề nào mà máy tính cổ điển có thể giải quyết. Và các kỹ sư vẫn đang cố gắng xây dựng một máy tính lượng tử hữu ích. Nhưng bài báo của Raz và Tal chứng minh rằng máy tính lượng tử và máy tính cổ điển thực sự là hai loại máy tính khác nhau—rằng ngay cả trong một thế giới nơi máy tính cổ điển đạt được thành công vượt xa những giấc mơ thực tế nhất, máy tính lượng tử vẫn đứng ở một vị thế vượt xa họ.
Các Lớp Lượng Tử
Một nhiệm vụ cơ bản của khoa học máy tính lý thuyết là phân loại các vấn đề vào các lớp phức tạp. Một lớp phức tạp chứa tất cả các vấn đề có thể giải quyết trong một nguồn lực nhất định, nơi nguồn lực đó là một cái gì đó như thời gian hoặc bộ nhớ.
Các nhà khoa học máy tính đã tìm ra một thuật toán hiệu quả, ví dụ, để kiểm tra xem một số có phải là số nguyên tố hay không. Tuy nhiên, họ không thể tìm ra một thuật toán hiệu quả để xác định các thừa số nguyên tố của các số lớn. Do đó, các nhà khoa học máy tính tin rằng (nhưng không thể chứng minh) rằng hai vấn đề đó thuộc về các lớp phức tạp khác nhau.
Hai lớp phức tạp nổi tiếng nhất là “P” và “NP.” P là tất cả các vấn đề mà máy tính cổ điển có thể giải quyết nhanh chóng. (“Có phải là số nguyên tố không?” thuộc P.) NP là tất cả các vấn đề mà máy tính cổ điển không nhất thiết phải giải quyết nhanh chóng, nhưng mà nếu có câu trả lời, họ có thể xác nhận nhanh chóng. (“Các thừa số nguyên tố của nó là gì?” thuộc NP.) Các nhà khoa học máy tính tin rằng P và NP là các lớp phức tạp khác nhau, nhưng chứng minh sự khác biệt đó thực sự là vấn đề khó nhất và quan trọng nhất trong lĩnh vực này.
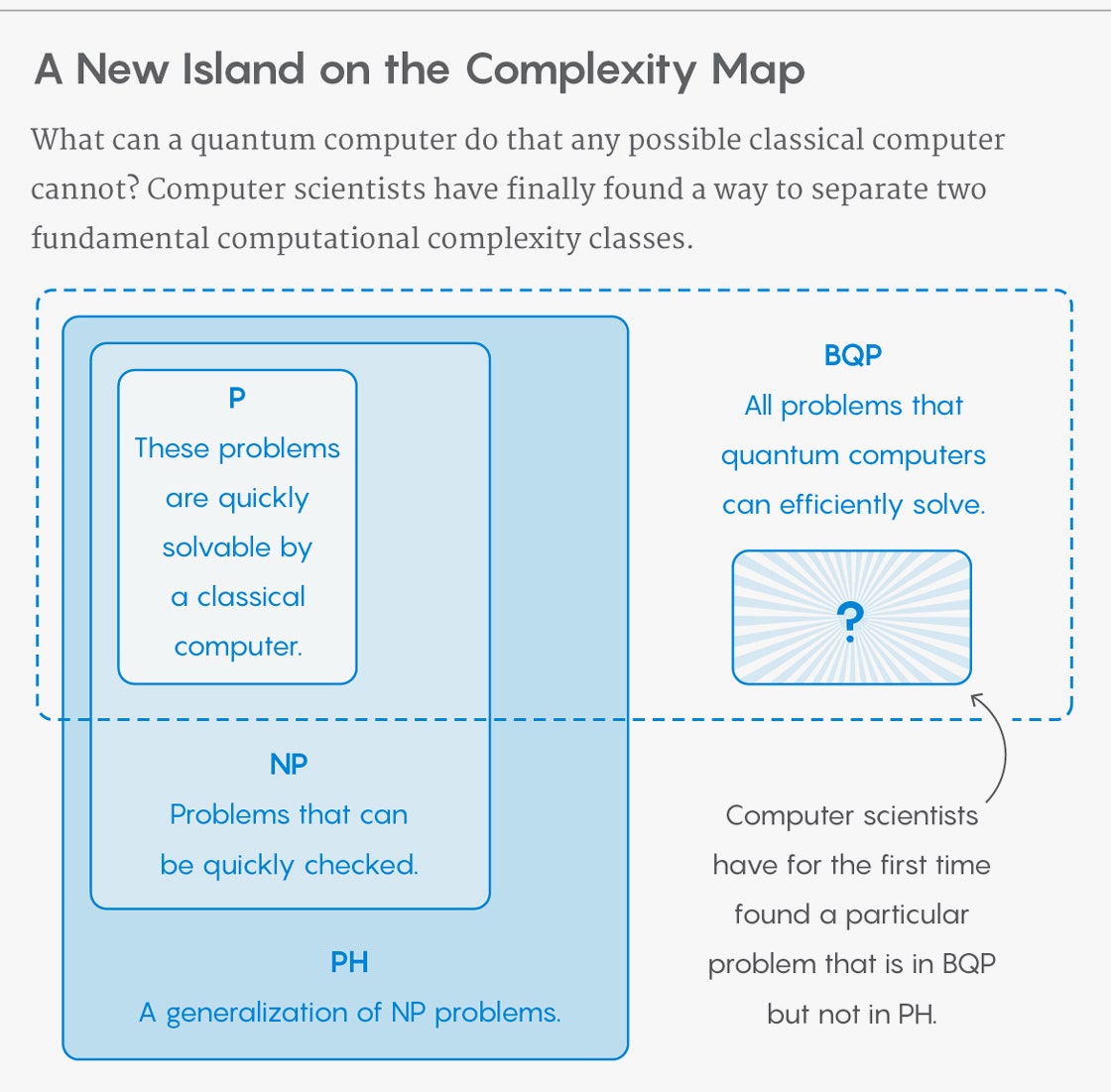
Năm 1993, các nhà khoa học máy tính Ethan Bernstein và Umesh Vazirani định nghĩa một lớp phức tạp mới mà họ gọi là BQP, viết tắt của “bounded-error quantum polynomial time.” Họ định nghĩa lớp này chứa tất cả các vấn đề quyết định—các vấn đề có câu trả lời là có hoặc không—mà máy tính lượng tử có thể giải quyết một cách hiệu quả. Cùng lúc đó, họ cũng chứng minh rằng máy tính lượng tử có thể giải quyết tất cả các vấn đề mà máy tính cổ điển có thể giải quyết. Nói cách khác, BQP chứa tất cả các vấn đề thuộc P.
Nhưng họ không thể xác định được liệu BQP chứa những vấn đề không thuộc một lớp vấn đề quan trọng khác được biết đến là “PH,” viết tắt của “polynomial hierarchy.” PH là sự tổng quát hóa của NP. Điều này có nghĩa là nó chứa tất cả các vấn đề mà bạn có được nếu bạn bắt đầu với một vấn đề thuộc NP và làm cho nó phức tạp hơn bằng cách đặt các câu như “tồn tại” và “cho tất cả.”1 Máy tính cổ điển ngày nay không thể giải quyết phần lớn các vấn đề thuộc PH, nhưng bạn có thể tưởng tượng PH như là lớp của tất cả các vấn đề mà máy tính cổ điển có thể giải quyết nếu P ngẫu nhiên bằng NP. Nói cách khác, so sánh BQP và PH là để xác định liệu máy tính lượng tử có ưu thế hơn máy tính cổ điển hay không, ngay cả khi máy tính cổ điển có thể (một cách không ngờ) giải quyết nhiều vấn đề hơn họ có thể hôm nay.
“PH là một trong những lớp phức tạp cổ điển cơ bản nhất,” nói Scott Aaronson, một nhà khoa học máy tính tại Đại học Texas tại Austin. “Vì vậy, chúng ta muốn biết, máy tính lượng tử nằm ở đâu trong thế giới lý thuyết phức tạp cổ điển?”
Cách tốt nhất để phân biệt giữa hai lớp phức tạp là tìm ra một vấn đề có thể chứng minh rằng nó thuộc một lớp nhưng không thuộc lớp khác. Tuy nhiên, do sự kết hợp giữa các rào cản cơ bản và kỹ thuật, việc tìm ra một vấn đề như vậy đã là một thách thức.
Nếu bạn muốn một vấn đề thuộc BQP nhưng không thuộc PH, bạn phải xác định điều gì đó mà “theo định nghĩa máy tính cổ điển không thể xác nhận câu trả lời một cách hiệu quả, chưa kể việc tìm ra nó,” như Aaronson nói. “Điều này loại bỏ rất nhiều vấn đề chúng ta nghĩ về trong khoa học máy tính.”
Hỏi Người Mở Đầu
Dưới đây là vấn đề. Hãy tưởng tượng bạn có hai bộ tạo số ngẫu nhiên, mỗi bộ tạo ra một chuỗi chữ số. Câu hỏi đối với máy tính của bạn là: Hai chuỗi này có hoàn toàn độc lập từ nhau, hay chúng có liên quan với nhau một cách ẩn (trong đó một chuỗi là “biến đổi Fourier” của chuỗi kia)? Aaronson giới thiệu vấn đề “forrelation” này vào năm 2009 và chứng minh rằng nó thuộc BQP. Điều này để lại bước khó khăn hơn, bước thứ hai—chứng minh rằng forrelation không thuộc PH.

Đó là những gì Raz và Tal đã làm, ở một khía cạnh cụ thể. Bài báo của họ đạt được điều được gọi là sự “tách biệt trực tuyến” (hoặc “hộp đen”) giữa BQP và PH. Đây là một loại kết quả phổ biến trong khoa học máy tính và là một điều mà các nhà nghiên cứu sử dụng khi cái họ thực sự muốn chứng minh vượt ra khỏi tầm tay.
Cách tốt nhất thực sự để phân biệt giữa các lớp phức tạp như BQP và PH là đo thời gian tính toán cần thiết để giải quyết một vấn đề trong mỗi lớp. Nhưng các nhà khoa học máy tính “không có một hiểu biết phức tạp, hoặc khả năng đo lường, về thời gian tính toán thực tế,” như Henry Yuen, một nhà khoa học máy tính tại Đại học Toronto, nói.
Do đó, thay vào đó, các nhà khoa học máy tính đo một điều khác mà họ hy vọng sẽ cung cấp cái nhìn về thời gian tính toán mà họ không thể đo được: Họ tính số lần mà máy tính cần tham vấn một “người mở đầu” để đưa ra câu trả lời. Người mở đầu giống như một người đưa gợi ý. Bạn không biết nó tạo ra gợi ý bằng cách nào, nhưng bạn biết chúng đáng tin cậy.
Nếu vấn đề của bạn là tìm hiểu xem hai bộ tạo số ngẫu nhiên có liên quan nhau một cách bí mật hay không, bạn có thể hỏi người mở đầu những câu hỏi như “Số thứ sáu từ mỗi bộ tạo số là gì?” Sau đó, bạn so sánh sức mạnh tính toán dựa trên số lượng gợi ý mà mỗi loại máy tính cần để giải quyết vấn đề. Máy tính cần nhiều gợi ý hơn là máy tính chậm hơn.
“Một cách nào đó, chúng ta hiểu mô hình này nhiều hơn. Nó nói nhiều hơn về thông tin hơn là tính toán,” nói Tal.

Bài báo mới của Raz và Tal chứng minh rằng máy tính lượng tử cần ít gợi ý hơn nhiều so với máy tính cổ điển để giải quyết vấn đề forrelation. Trên thực tế, máy tính lượng tử chỉ cần một gợi ý, trong khi ngay cả với số lượng gợi ý không giới hạn, không có thuật toán nào trong PH có thể giải quyết vấn đề. “Điều này có nghĩa là có một thuật toán lượng tử rất hiệu quả giải quyết vấn đề đó,” nói Raz. “Nhưng nếu chỉ xem xét thuật toán cổ điển, thậm chí nếu bạn đến với các lớp thuật toán cổ điển rất cao, chúng cũng không thể.” Điều này xác lập rằng với người mở đầu, forrelation là một vấn đề thuộc BQP nhưng không thuộc PH.
Raz và Tal gần như đạt được kết quả này gần bốn năm trước, nhưng họ không thể hoàn thành một bước trong bằng chứng của mình. Sau đó chỉ một tháng trước đây, Tal nghe một buổi báo cáo về một bài báo mới về bộ tạo số ngẫu nhiên giả mạo và nhận ra rằng các kỹ thuật trong bài báo đó chính là điều mà anh ấy và Raz cần để hoàn thành công trình của mình. “Đây là mảnh ghép bị mất,” nói Tal.
Công việc cung cấp một đảm bảo chắc chắn rằng máy tính lượng tử tồn tại trong một lĩnh vực tính toán khác biệt so với máy tính cổ điển (ít nhất là đối với một người mở đầu). Ngay cả trong một thế giới nơi P bằng NP—một nơi mà vấn đề người du lịch đơn giản như tìm một đường thích hợp trên một bảng tính—bằng chứng của Raz và Tal chứng minh rằng vẫn có những vấn đề mà chỉ máy tính lượng tử có thể giải quyết.
“Ngay cả khi P bằng NP, thậm chí khi đưa ra giả thiết mạnh mẽ đó,” nói Fortnow, “điều đó cũng không đủ để hiểu về tính toán lượng tử.”
Bài viết gốc được tái in với sự cho phép từ Quanta Magazine, một tờ báo độc lập về biên tập thuộc Quỹ Simons với sứ mệnh tăng cường sự hiểu biết của công chúng về khoa học bằng cách báo cáo về sự phát triển và xu hướng nghiên cứu trong toán học và các ngành khoa học tự nhiên và y sinh.
0 Thích